액체나 기체 속에서 작은 입자들이 외부의 다른 작용 없이 불규칙하게 '표류'하는 것을 '브라운 운동'이라고 한다.
1827년 스코틀랜드 식물학자 로버트 브라운이 물에 띄운 꽃가루 입자를 관찰하다가 처음 발견해 이름이 붙여졌다. 연기가 공기중에 퍼져나가는 것이나 잉크가 물 속에서 퍼져나가는 것들이 모두 브라운 운동의 예이다.
브라운 운동을 설명하는 방정식은 아인슈타인이 처음 제시했으며 프랑스의 물리화학자인 페랭은 아인슈타인의 방정식을 실험으로 증명해 1926년에 노벨 물리학상을 받았다.
하지만 아이슈타인의 방정식은 입자의 크기가 크고 액체가 균일할 때는 정확했지만 여러 분자나 입자가 섞여 있는 복잡 액체에서는 맞지 않았다. 복잡 액체에서 입자 열운동을 설명하는 것은 현대 통계물리학의 난제 중 하나였다.
한국연구재단은 중앙대학교 성재영·김지현 교수가 세포환경과 같은 복잡 액체에서도 일관되게 성립하는 분자들의 수송방정식을 발견했다고 13일 밝혔다.
이상엽 교수(서울대), 김준수 교수(이화여대), 성봉준 교수(서강대)가 함께 참여했으며 연구논문은 저명 국제학술지 '미국국립학술원회보(PNAS)'에 6월 11일 게재됐다.
최근 크게 발전한 고해상도 단일분자 실험법과 분자 동력학 시뮬레이션 방법을 통해 복잡한 유체 내의 분자 운동을 관찰할 수 있게 되면서 아인슈타인의 브라운 운동 이론으로 설명할 수 없는 현상들이 관찰됐다.
복잡한 액체 속 입자 운동은 시간에 따라 양상이 변화하는데 그 양상이 복잡 액체의 종류에 관계없이 비슷했다. 입자들은 아주 짧은 시간 동안은 총알처럼 관성운동을 하지만, 곧 매우 느린 아확산운동과 확산운동을 차례로 한다.
시간에 따라 입자의 이동거리가 정규분포에서 벗어나는 정도는 늘어나다 다시 줄어든다. 이 현상은 아인슈타인의 브라운 운동 이론이나 그 후 등장한 많은 이론들로도 설명할 수 없었다.
성재영 교수 연구팀은 복잡한 액체 속 입자의 이동을 일관적으로 설명하기 위해 주변의 미시적 환경에 따라 운동성이 바뀌는 무작위 운동입자(random walker)모델을 제안했다.
환경에 따라 운동성이 변하는 무작위 운동입자 모델로부터 아인슈타인과 다른 새로운 수송 방정식을 얻었고, 이 방정식의 정확한 해가 세포 속 환경, 고분자 유체, 과냉각수, 이온액체 등에서 발견되는 다양한 비정규분포 수송 현상을 정확하고 일관되게 설명할 수 있다는 것을 증명했다.
성재영 교수는 "이번 연구는 통계물리학 분야의 난제인 복잡 유체 내 분자 열운동과 수송 현상을 설명할 수 있는 일반적인 방정식과 해를 찾아낸 것"이라며, "세포 내 효소와 생체 고분자들의 열운동을 통해 일어나는 다양한 생명 현상들을 물리화학적으로 이해하고 예측하는 데 우선 응용할 계획"이라고 밝혔다.
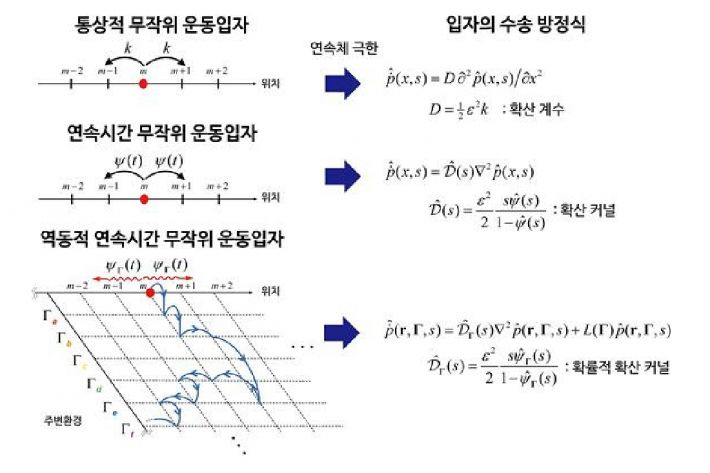기존 무작위 운동입자 모델과 새롭게 제시한 역동적 연속시간 무작위 운동입자 모델 <한국연구재단 제공="">